|
|
|
|
Celestial navigation is finding your position using the stars, sun,
moon, and planets. Although easy in concept, in practice it is
complicated to determine your position on Earth; this page will
try to explain the principle, without the math.
A FixA fix is defined as the intersection of two or more lines of position. In piloting, a line of position or LOP can be a compass bearing to a known point on land, such as a lighthouse; when plotted on a chart, that bearing from the lighthouse represents a line that your ship must be on. A crossing line of position from another object produces a fix; additional lines of position verify the fix by crossing on or near the intersection point. A running fix uses a single line of position advanced with the dead reckoning (DR) position to obtain crossing bearings over time from a single navigation aid; similarly, LOPs may be advanced or retarded with the DR to compensate for not having been measured simultaneously. Due to the long time it takes to complete a set of celestial observations, advancing and retarding LOPs is a common feature of a celestial fix.The Celestial SphereTo the celestial navigator, the Earth is a perfect sphere. The stars are on the celestial sphere-- remember globes you may have seen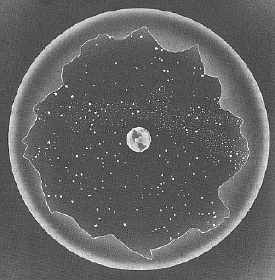 with the Earth surrounded by
a clear sphere with the stars printed on it: that is the celestial
sphere. The stars are fixed upon the sphere in relation to each
other and thus are called fixed stars; 57 of them are
considered bright enough for use in celestial navigation. In fact
the fixed stars do move, but so slowly that only study of an almanac
would reveal it. Planets as a class move among the fixed
stars; the navigational planets are Mercury, Venus, Mars, Jupiter,
Saturn, the Moon, and the Sun. They confine themselves to a band
that extends 8° on either side of the ecliptic, the
apparent path that the sun follows through the sky. The ecliptic
is tilted relative to the Earth's equator due to the tilt of the
Earth's axis. with the Earth surrounded by
a clear sphere with the stars printed on it: that is the celestial
sphere. The stars are fixed upon the sphere in relation to each
other and thus are called fixed stars; 57 of them are
considered bright enough for use in celestial navigation. In fact
the fixed stars do move, but so slowly that only study of an almanac
would reveal it. Planets as a class move among the fixed
stars; the navigational planets are Mercury, Venus, Mars, Jupiter,
Saturn, the Moon, and the Sun. They confine themselves to a band
that extends 8° on either side of the ecliptic, the
apparent path that the sun follows through the sky. The ecliptic
is tilted relative to the Earth's equator due to the tilt of the
Earth's axis.
Positions on Earth are measured in latitude, from 0° at the equator to 90° north and south at the poles, and longitude, running from pole to pole and measured from 0° at the Greenwich meridian (another term for line of longitude) to 180° east and west. Positions on the celestial sphere have corresponding latitude and longitude; the celestial equator is projected out from the Earth's equator, and declination is measured north and south from it to the celestial poles at 90°. Longitude on the celestial sphere is called hour angle, and is measured west through 360° from the starting point. The starting point marks where the Sun crosses the celestial equator in the spring, the vernal equinox, and the angle from it to a celestial body is called the sidereal hour angle, or SHA. This starting point is called the first point of Aries, because when the point was named, the Sun was entering the constellation Aries (due to precession, this is no longer the case). In the navigator's view of the Earth and celestial sphere, the Earth is stationary and the celestial sphere rotates around it, completing one rotation about every 24 hours. At this rate, the celestial sphere rotates one degree every four minutes. Astronomers measure celestial longitude east from the first point of Aries, and use time units (hours, minutes, and seconds of time) rather than degrees. This is called right ascension or RA, but is not used by the celestial navigator. The Basic ConceptImagine you are standing on the Earth, and one of the navigational stars is directly above you. If you know the time, you can use the Nautical Almanac to find the position of the star on the celestial sphere, and then the position of the spot directly beneath it on the Earth. That's your location. In this situation, if you measured the angle between the horizon and the star (using a sextant, which is merely a tool to accurately measure angles), it would be 90° (less the various corrections we will ignore for now). The line of position (LOP) for a star at an angular altitude of 90° is in fact a dot, called the geographic position, or GP.
Now, in your mind picture, step back until the angle of the star
above the horizon is 89°. The LOP in this case is a small
circle around the GP; someone standing anywhere on this circle
would get the same measurement of 89°.
Over What was needed was a way to accurately plot just a small segment of the circle of equal altitude: a small segment of a circle thousands of miles in diameter could accurately be represented by a straight line on a chart. Altitude InterceptThe navigational triangle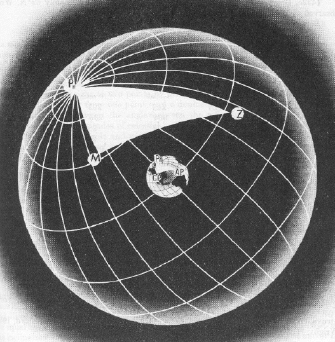 is a triangle formed on the surface of the Earth; its three points
are the Pole (either North or South, depending on your position),
the GP of the observed star, and your position. Knowing all three
points allows you to calculate the length of the leg from your
position to the GP, and the angle between the GP and the Pole,
which can be reduced to the GP's bearing. Now calculated by computer
or even calculator, the solving of this navigational triangle can
be done by publications called Sight Reduction Tables, which
give the solutions for whole degree positions of own ship and GP.
Interpolation could then be used to determine the exact solution.
is a triangle formed on the surface of the Earth; its three points
are the Pole (either North or South, depending on your position),
the GP of the observed star, and your position. Knowing all three
points allows you to calculate the length of the leg from your
position to the GP, and the angle between the GP and the Pole,
which can be reduced to the GP's bearing. Now calculated by computer
or even calculator, the solving of this navigational triangle can
be done by publications called Sight Reduction Tables, which
give the solutions for whole degree positions of own ship and GP.
Interpolation could then be used to determine the exact solution.
There is a problem you may have noticed with the above procedure: it assumes own ship's position is known. Isn't that what we are trying to determine? Very true: what is used in the calculations is the ships DR, or Dead Reckoning position; the best estimate of the ship's position based on distance and direction traveled from the last fix. It is assumed that this position is not absolutely accurate, but it only needs to be close enough that the celestial LOP we plot will fall within the bounds of the chart we are using. So if we're using a not-accurate position to start with, why not fudge it a little, so that when we use this fudged DR in the Sight Reduction Tables, all the numbers come out to even degrees and we don't have to interpolate at all? And this is exactly what is done. The "fudged" DR is called the Assumed Position or AP. It is plotted on the chart, and the Sight Reduction Tables are used to determine the bearing to the GP of the star; this is plotted on the chart through the AP: the GP of the star is somewhere on that line (but well off the chart). The tables also tell us the distance to the GP, using angular values (nautical miles expressed in degrees and minutes of arc): this is known as the Altitude Intercept. Therefore, we know that for a ship positioned at the AP at the exact time of the celestial observation, the GP of the star is at a particular bearing and the star appeared at a particular angle to the horizon.
Now The question becomes, do we plot the LOP on the bearing towards the GP of the star from the AP, or away from the GP? Remembering our mental picture of the circular LOPs on the surface of the Earth will help: if a star is measured at an altitude of 80° above the horizon, it will be high in the sky and the LOP will be very small (at 90° it would be a dot: we would be directly below the star at its Geographic Position). At 60°, the same star will be closer to the horizon, and the LOP would be much larger. So, the smaller the angle above the horizon, the further away the LOP will be from the star's GP. Applying this to our problem, if the angle for the assumed position, our calculated angle, is 60°, and the angle we actually measured, our observed angle, is 59°, the actual LOP must be further from the GP than the AP. The rule is commonly remembered by the saying, "Calculated Greater, Away": if your calculated angle is greater than your observed angle, plot the LOP away from the direction of the GP. This rule is further remembered as "CGA", which also stands for "Coast Guard Academy". Another memory aid, using the opposite sense, is "Ho Mo To", for Ho (observed altitude [I cheat and think of it as height observed]) More Toward, or, if the observed altitude is more than the calculated altitude, it is plotted toward the GP.
We've done it: All graphics on this page have been scanned from DMA Pub No. 9, The American Practical Navigator (Bowditch), Volume I, 1977 edition |
| HOME | Articles | Sea Stories | Book List |
| Links | Deck Log | Contribute | About |